The EPJLA Binary Counter
Maximize and hit "f" to center.
As if Langton's Ant didn't have enough to do. Along came Ed Pegg, Jr. and asked the poor guy to count! Ed discovered that by changing the rules a smidge the ant's droppings will go through a binary counting sequence. The EPJLA rules are
Second, many paths through the Turing cells never occur. Langton's original ant can enter from the N, S, E, or W, and turn either direction from each entry point. The EPJLAnt enters only from the W or S in the top row, and only from the E or N in the bottom row. In the original version many cross elements are needed, these being of the more difficult WireWorld elements to construct. Ed's ant needs no crosses.
No technical details, only English.
Three paths through each cell are required. For the top row they are
For the bottom row, replace E with W, W with E, N with S, and S with N. If you're a Turing purist please skip the rest of this paragraph. With the original ant every Turing cell was identical to every other one and identical when rotated by 1/4 and 1/2 turn. That approach could have been kept with EPJLA also, but at the expense of many never-to-be-used paths. I took the simpler approach of minimizing the logic, and using a 180-degree rotated top row as the bottom row.
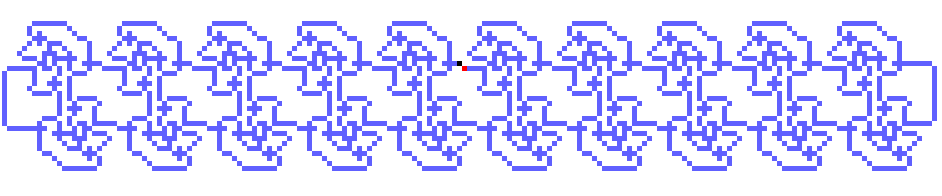
The following counts from 0 through 31, then repeats. It takes slighly over 5000 ticks to go from 0 to 0.

The MCell Source Code. You'll need Mirek's Cellabration to run it.